_images/uqlm_flow_ds.png _images/uqlm_flow_ds_dark.png

uqlm: Uncertainty Quantification for Language Models#

Get Started → | View Examples →

UQLM is a Python library for Large Language Model (LLM) hallucination detection using state-of-the-art uncertainty quantification techniques.

Hallucination Detection#

UQLM provides a suite of response-level scorers for quantifying the uncertainty of Large Language Model (LLM) outputs. Each scorer returns a confidence score between 0 and 1, where higher scores indicate a lower likelihood of errors or hallucinations. We categorize these scorers into four main types:

Comparison of Scorer Types#

Scorer Type

Added Latency

Added Cost

Compatibility

Off-the-Shelf / Effort

Black-Box Scorers

⏱️ Medium-High (multiple generations & comparisons)

💸 High (multiple LLM calls)

🌍 Universal (works with any LLM)

✅ Off-the-shelf

White-Box Scorers

⚡ Minimal (token probabilities already returned)

✔️ None (no extra LLM calls)

🔒 Limited (requires access to token probabilities)

✅ Off-the-shelf

LLM-as-a-Judge Scorers

⏳ Low-Medium (additional judge calls add latency)

💵 Low-High (depends on number of judges)

🌍 Universal (any LLM can serve as judge)

✅ Off-the-shelf; Can be customized

Ensemble Scorers

🔀 Flexible (combines various scorers)

🔀 Flexible (combines various scorers)

🔀 Flexible (combines various scorers)

✅ Off-the-shelf (beginner-friendly); 🛠️ Can be tuned (best for advanced users)

Long-Text Scorers

⏱️ High-Very high (multiple generations & claim-level comparisons)

🔀 💸 High (multiple LLM calls)

🔀 🌍 Universal

✅ Off-the-shelf

1. Black-Box Scorers (Consistency-Based)#

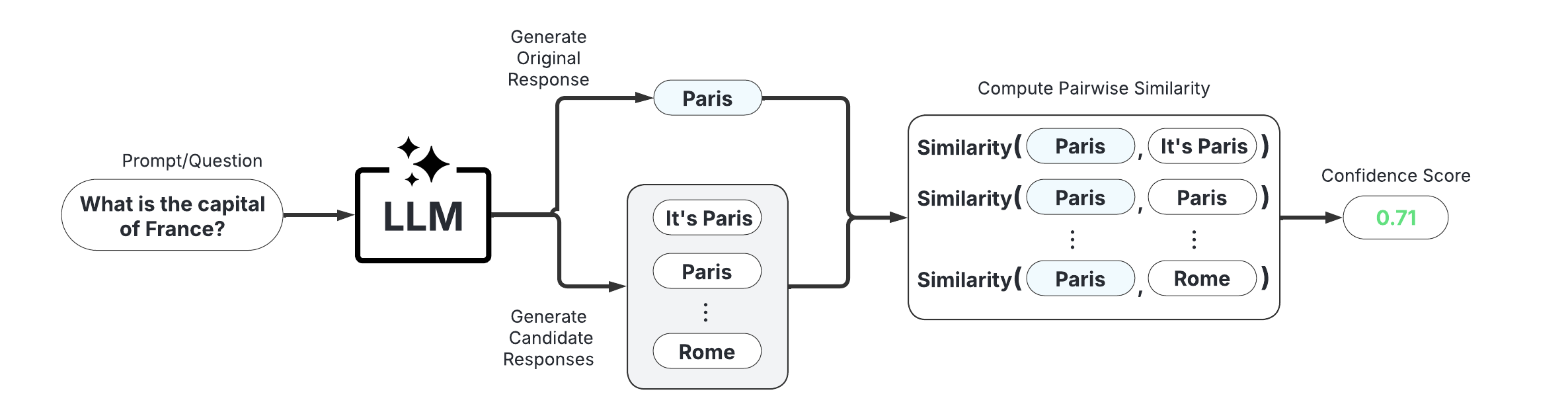
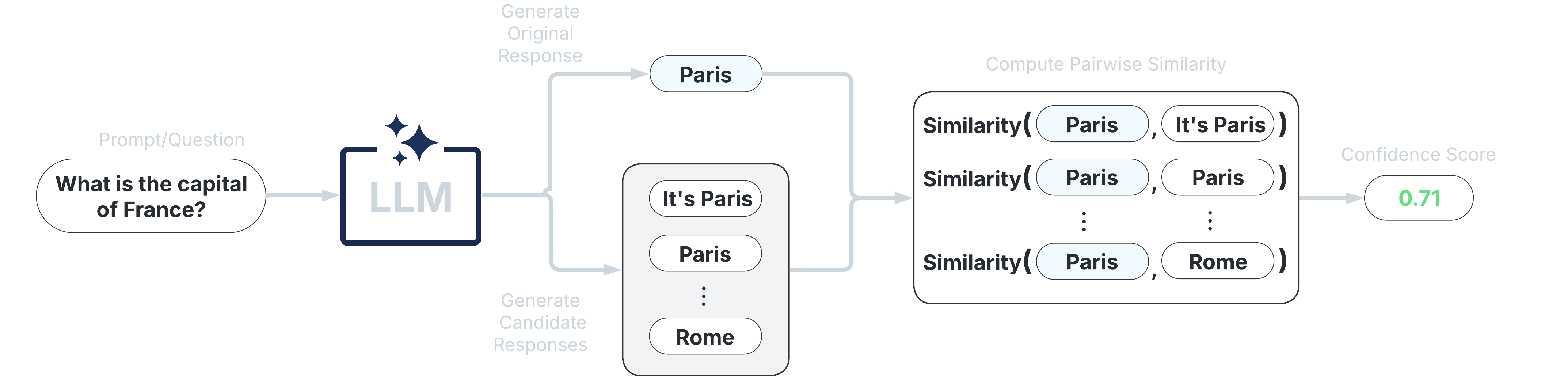
_images/black_box_graphic.png _images/black_box_graphic_dark.png

These scorers assess uncertainty by measuring the consistency of multiple responses generated from the same prompt. They are compatible with any LLM, intuitive to use, and don’t require access to internal model states or token probabilities.

2. White-Box Scorers (Token-Probability-Based)#

_images/white_box_graphic.png _images/white_box_graphic_dark.png

These scorers leverage token probabilities to estimate uncertainty. They offer single-generation scoring, which is significantly faster and cheaper than black-box methods, but require access to the LLM’s internal probabilities, meaning they are not necessarily compatible with all LLMs/APIs. The following single-generation scorers are available:

UQLM also offers sampling-based white-box methods, which incur higher cost and latency, but tend have superior hallucination detection performance. The following sampling-based white-box scorers are available:

Lastly, the P(True) scorer is offered, which is a self-reflection method that requires one additional generation per response.

3. LLM-as-a-Judge Scorers#

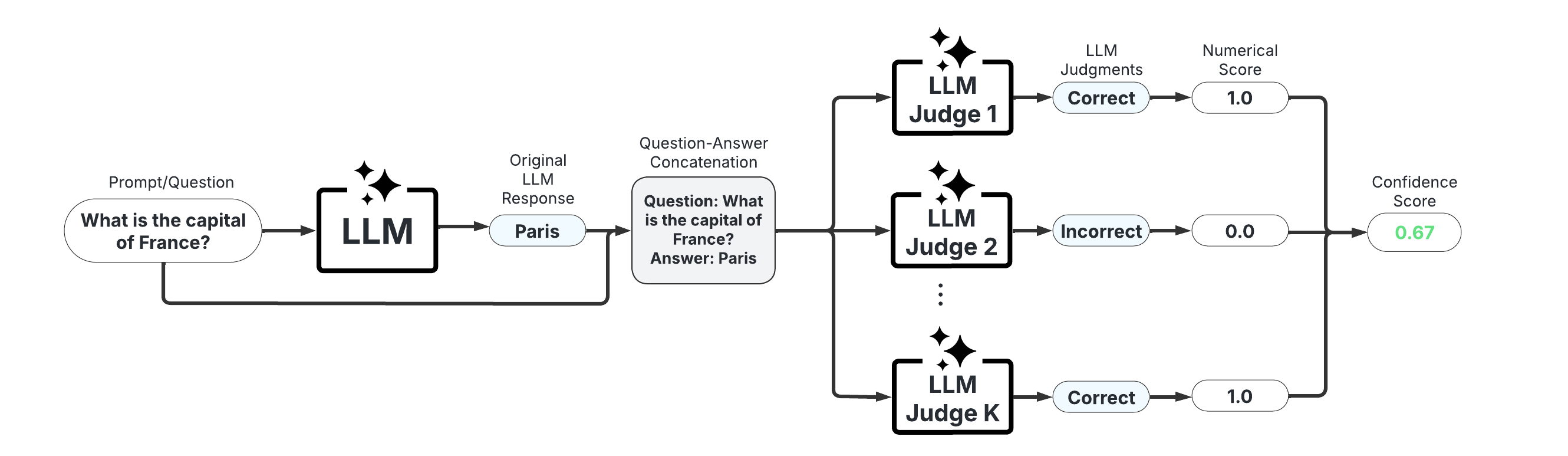
_images/judges_graphic.png _images/judges_graphic_dark.png

These scorers use one or more LLMs to evaluate the reliability of the original LLM’s response. They offer high customizability through prompt engineering and the choice of judge LLM(s).

4. Ensemble Scorers#

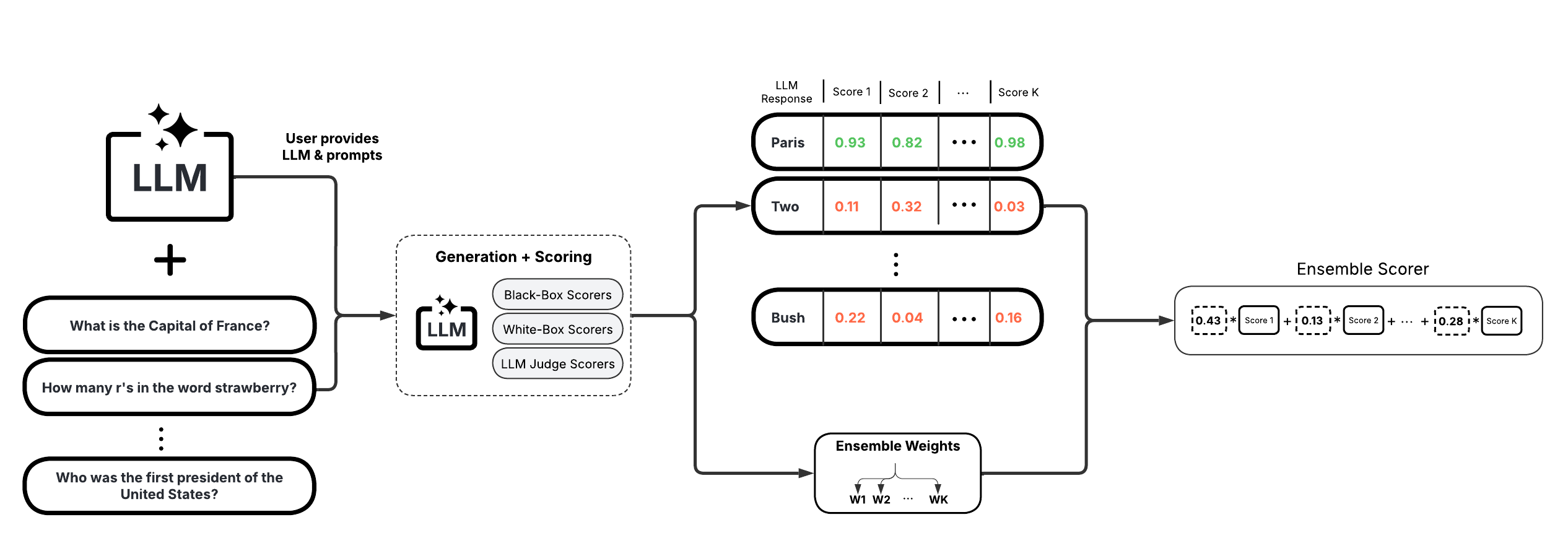
_images/uqensemble_generate_score.png _images/uqensemble_generate_score_dark.png

These scorers leverage a weighted average of multiple individual scorers to provide a more robust uncertainty/confidence estimate. They offer high flexibility and customizability, allowing you to tailor the ensemble to specific use cases.

5. Long-Text Scorers (Claim-Level)#

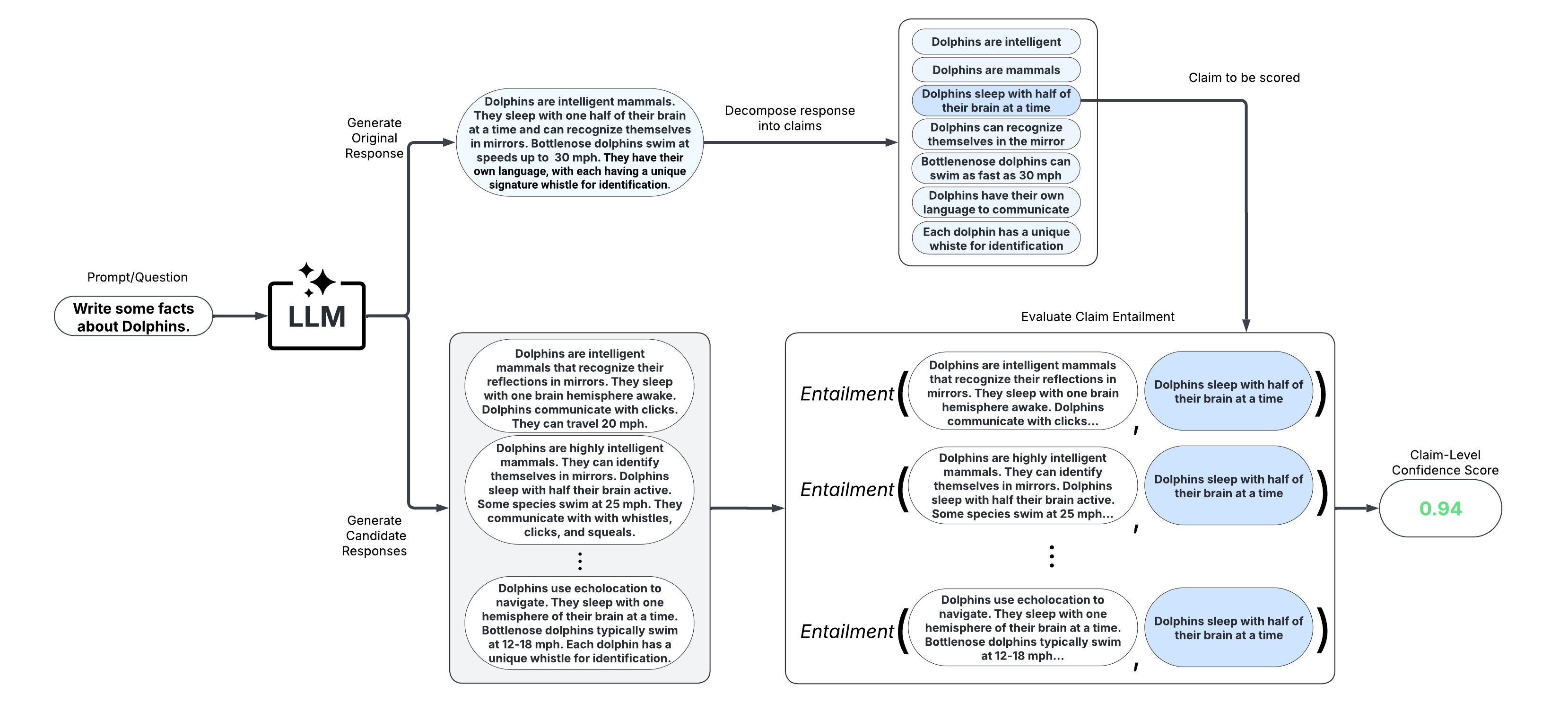
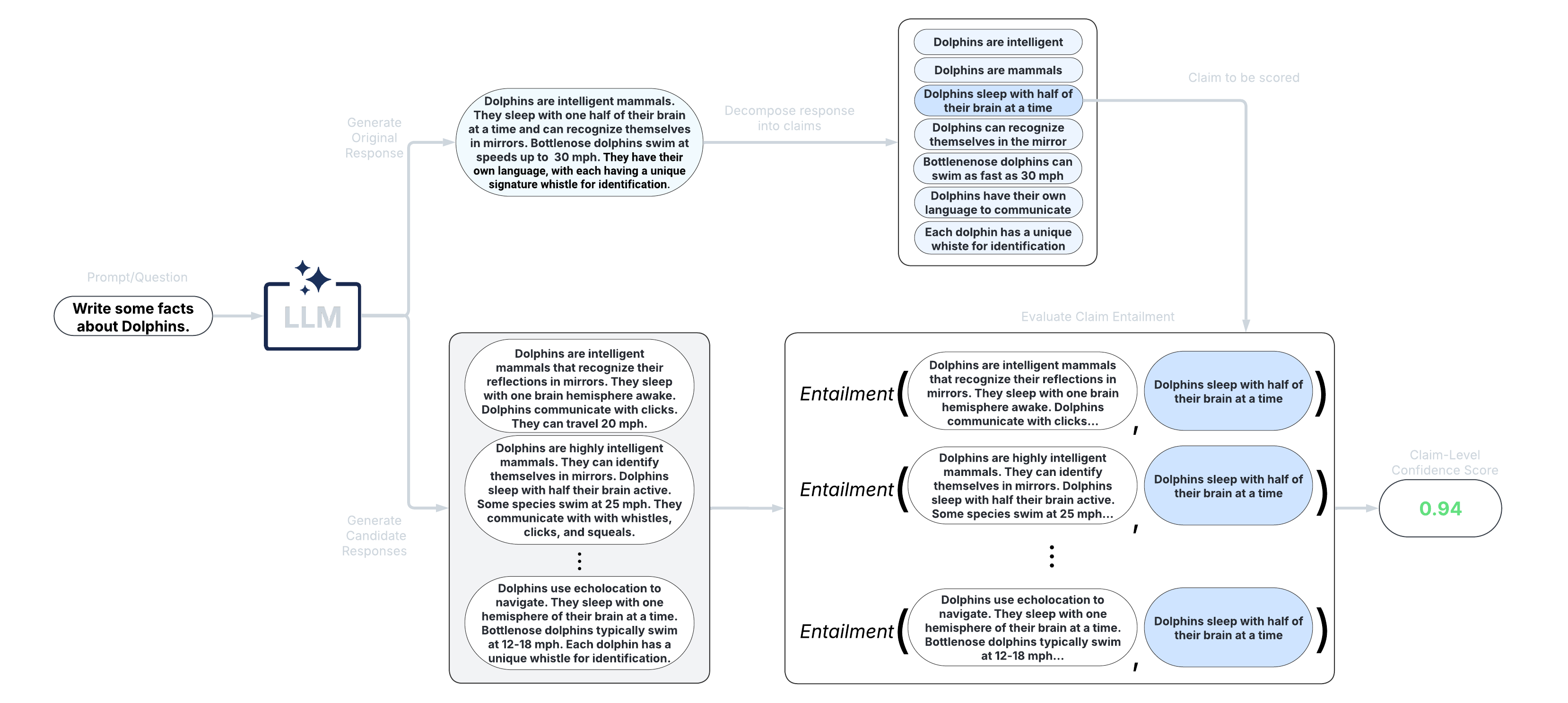
_images/luq_example.png _images/luq_example_dark.png

These scorers take a fine-grained approach and score confidence/uncertainty at the claim or sentence level. An extension of black-box scorers, long-text scorers sample multiple responses to the same prompt, decompose the original response into claims or sentences, and evaluate consistency of each original claim/sentence with the sampled responses.

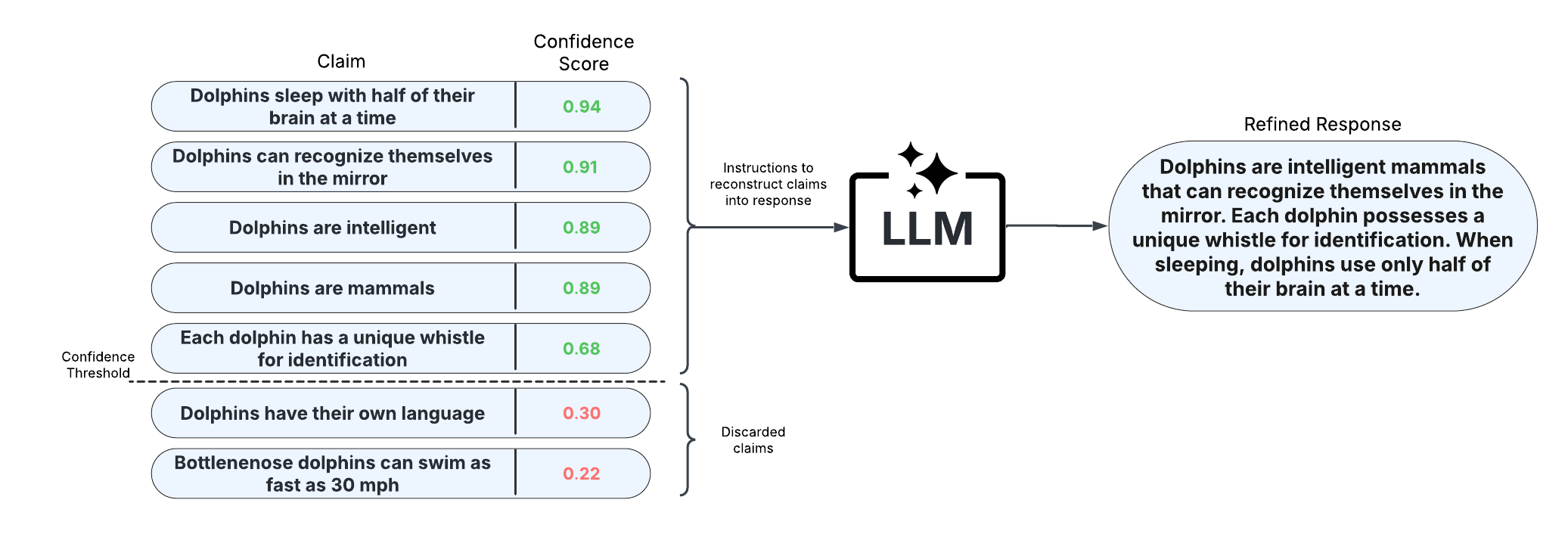
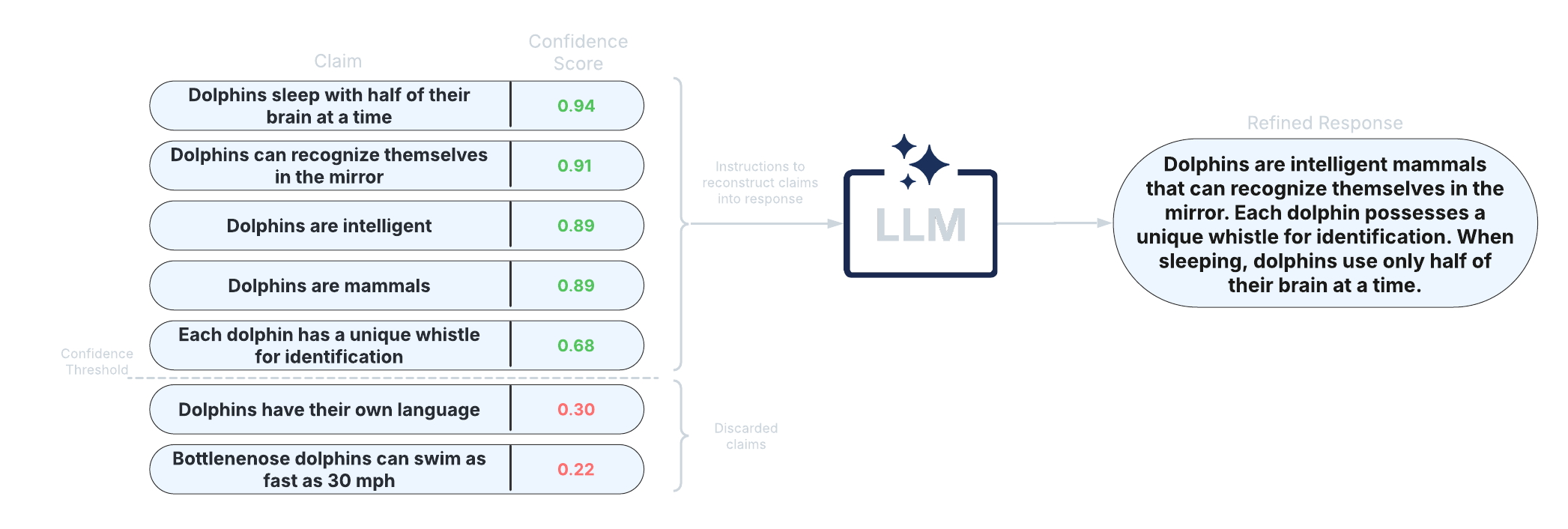
_images/uad_graphic.png _images/uad_graphic_dark.png

After scoring claims in the response, the response can be refined by removing claims with confidence scores less than a specified threshold and reconstructing the response from the retained claims. This approach allows for improved factual precision of long-text generations.

Contents#