🎯 Tunable Ensemble for LLM Uncertainty (Advanced)

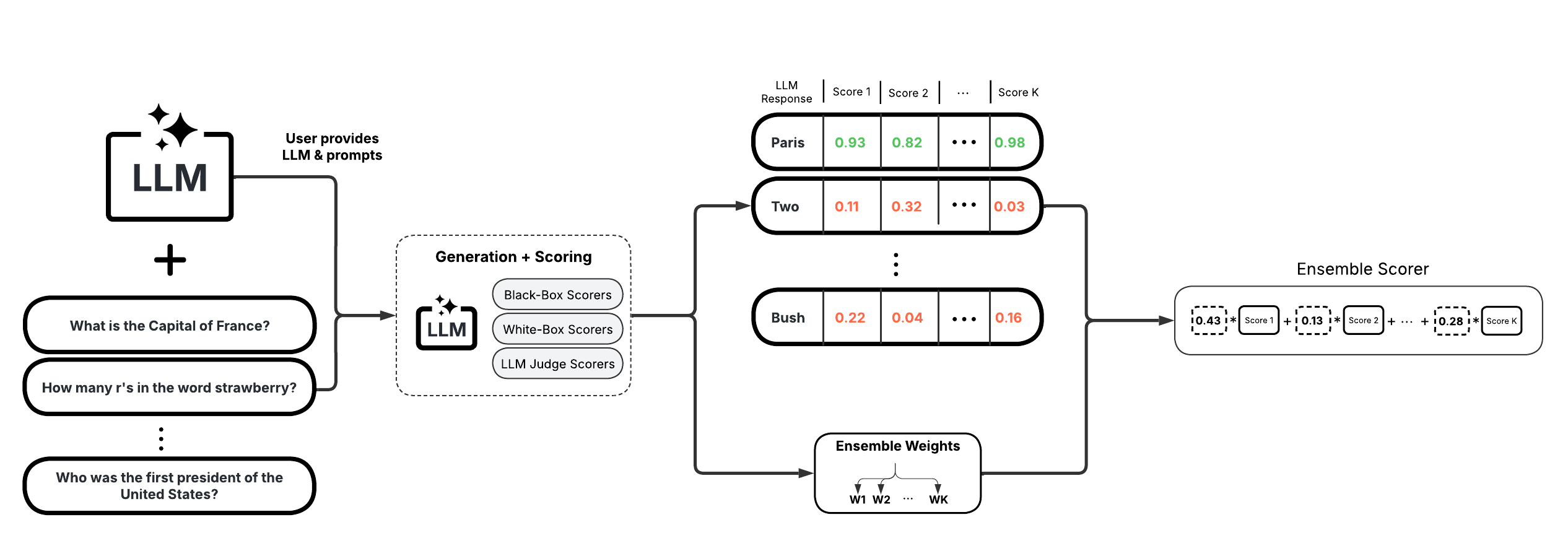
Ensemble UQ methods combine multiple individual scorers to provide a more robust uncertainty estimate. They offer high flexibility and customizability, allowing you to tailor the ensemble to specific use cases. This ensemble can leverage any combination of black-box, white-box, or LLM-as-a-Judge scorers offered by uqlm. Below is a list of the available scorers:

Black-Box Scorers

• Discrete Semantic Entropy (Farquhar et al., 2024; Kuhn et al., 2023)

• Number of Semantic Sets (Lin et al., 2024; Vashurin et al., 2025; Kuhn et al., 2023)

• Non-Contradiction Probability (Chen & Mueller, 2023; Lin et al., 2024; Manakul et al., 2023)

• Entailment Probability (Lin et al., 2025; Chen & Mueller, 2023)

• Exact Match (Cole et al., 2023; Chen & Mueller, 2023)

• BERTScore (Manakul et al., 2023; Zheng et al., 2020)

• Normalized Cosine Similarity (Shorinwa et al., 2024; HuggingFace)

White-Box Scorers (select single generation scorers only; more coming soon)

• Minimum token probability (Manakul et al., 2023)

• Length-Normalized Joint Token Probability (Malinin & Gales, 2021)

LLM-as-a-Judge Scorers

• Categorical LLM-as-a-Judge (Manakul et al., 2023; Chen & Mueller, 2023; Luo et al., 2023)

• Continuous LLM-as-a-Judge (Xiong et al., 2024)

• Likert Scale LLM-as-a-Judge (Bai et al., 2023)

📊 What You’ll Do in This Demo

1

Set up LLM and prompts.

Set up LLM instance and load example data prompts.

2

Tune Ensemble Weights

Tune the ensemble weights on a set of tuning prompts. You will execute a single UQEnsemble.tune() method that will generate responses, compute confidence scores, and optimize weights using a provided answer key corresponding to the provided questions.

3

Generate LLM Responses and Confidence Scores with Tuned Ensemble.

Generate and score LLM responses to the example questions using the tuned UQEnsemble() object.

4

Evaluate Hallucination Detection Performance.

Visualize LLM accuracy at different thresholds of the ensemble score that combines various scorers. Compute precision, recall, and F1-score of hallucination detection.

⚖️ Advantages & Limitations

Pros

• Highly Flexible: Versatile and adaptable to various tasks and question types.

• Highly Customizable: Ensemble weights can be tuned for optimal performance on a specific use case.

Cons

• Requires More Setup: Not quite “off-the-shelf”; requires some effort to configure and tune the ensemble.

• Best for Advanced Users: Optimizing the ensemble requires a deeper understanding of the individual scorers.

import numpy as np
from sklearn.metrics import precision_score, recall_score, f1_score

from uqlm import UQEnsemble
from uqlm.utils import load_example_dataset, math_postprocessor, plot_model_accuracies, plot_ranked_auc

1. Set up LLM and Prompts

In this demo, we will illustrate this approach using a set of math questions from the SVAMP benchmark. To implement with your use case, simply replace the example prompts with your data.

# Load example dataset (svamp)
svamp = load_example_dataset("svamp", n=200)
svamp.head()

Loading dataset - svamp...
Processing dataset...
Dataset ready!

	question	answer
0	There are 87 oranges and 290 bananas in Philip...	145
1	Marco and his dad went strawberry picking. Mar...	19
2	Edward spent $ 6 to buy 2 books each book cost...	3
3	Frank was reading through his favorite book. T...	198
4	There were 78 dollars in Olivia's wallet. She ...	63

svamp_tune = svamp.iloc[0:100]
svamp_test = svamp.iloc[100:200]

# Define prompts
MATH_INSTRUCTION = "When you solve this math problem only return the answer with no additional text.\n"
tune_prompts = [MATH_INSTRUCTION + prompt for prompt in svamp_tune.question]
test_prompts = [MATH_INSTRUCTION + prompt for prompt in svamp_test.question]

In this example, we use ChatVertexAI and AzureChatOpenAI to instantiate our LLMs, but any LangChain Chat Model may be used. Be sure to replace with your LLM of choice.

# import os
# import sys
# !{sys.executable} -m pip install python-dotenv
# !{sys.executable} -m pip install langchain-openai

# # User to populate .env file with API credentials. In this step, replace with your LLM of choice.
from dotenv import load_dotenv, find_dotenv
from langchain_openai import AzureChatOpenAI

load_dotenv(find_dotenv())
gpt4o_mini = AzureChatOpenAI(deployment_name="gpt-4o-mini", openai_api_type="azure", openai_api_version="2024-02-15-preview")

# import sys
# !{sys.executable} -m pip install langchain-google-vertexai
from langchain_google_vertexai import ChatVertexAI

gemini_flash = ChatVertexAI(model_name="gemini-2.5-flash")

2. Tune Ensemble

UQEnsemble() - Ensemble of uncertainty scorers

📋 Class Attributes

Parameter	Type & Default	Description
llm	BaseChatModeldefault=None	A langchain llm BaseChatModel. User is responsible for specifying temperature and other relevant parameters to the constructor of the provided llm object.
scorers	Listdefault=None	Specifies which black-box, white-box, or LLM-as-a-Judge scorers to include in the ensemble. List containing instances of BaseChatModel, LLMJudge, black-box scorer names from [‘semantic_negentropy’, ‘noncontradiction’,’exact_match’, ‘bert_score’, ‘cosine_sim’, ‘entailment’, ‘num_semantic_sets’], or white-box scorer names from [“normalized_probability”, “min_probability”]. If None, defaults to the off-the-shelf BS Detector ensemble by Chen & Mueller, 2023 which uses components [“noncontradiction”, “exact_match”,”self_reflection”] with respective weights of [0.56, 0.14, 0.3].
device	str or torch.devicedefault=”cpu”	Specifies the device that NLI model use for prediction. Only applies to ‘semantic_negentropy’, ‘noncontradiction’ scorers. Pass a torch.device to leverage GPU.
use_best	booldefault=True	Specifies whether to swap the original response for the uncertainty-minimized response among all sampled responses based on semantic entropy clusters. Only used if scorers includes ‘semantic_negentropy’ or ‘noncontradiction’.
system_prompt	str or Nonedefault=”You are a helpful assistant.”	Optional argument for user to provide custom system prompt for the LLM.
max_calls_per_min	intdefault=None	Specifies how many API calls to make per minute to avoid rate limit errors. By default, no limit is specified.
use_n_param	booldefault=False	Specifies whether to use n parameter for BaseChatModel. Not compatible with all BaseChatModel classes. If used, it speeds up the generation process substantially when num_responses is large.
postprocessor	callabledefault=None	A user-defined function that takes a string input and returns a string. Used for postprocessing outputs.
sampling_temperature	floatdefault=1	The ‘temperature’ parameter for LLM model to generate sampled LLM responses. Must be greater than 0.
weights	list of floatsdefault=None	Specifies weight for each component in ensemble. If None, and scorers is not None, and defaults to equal weights for each scorer. These weights get updated with tune method is executed.
nli_model_name	strdefault=”microsoft/deberta-large-mnli”	Specifies which NLI model to use. Must be acceptable input to AutoTokenizer.from_pretrained() and AutoModelForSequenceClassification.from_pretrained().
scoring_templates	intdefault=None	Specifies which off-the-shelf template to use for each judge. Four off-the-shelf templates offered: incorrect/uncertain/correct (0/0.5/1), incorrect/correct (0/1), continuous score (0 to 1), and likert scale score (1-5 scale, normalized to 0/0.25/0.5/0.75/1). These templates are respectively specified as ‘true_false_uncertain’, ‘true_false’, ‘continuous’, and ‘likert’. If specified, must be of equal length to judges list. Defaults to ‘true_false_uncertain’ template used by Chen and Mueller (2023) for each judge.
return_responses	strdefault=”all”	If a postprocessor is used, specifies whether to return only postprocessed responses, only raw responses, or both. Specified with ‘postprocessed’, ‘raw’, or ‘all’, respectively.

🔍 Parameter Groups

🧠 LLM-Specific

• llm

• system_prompt

• sampling_temperature

📊 Confidence Scores

• scorers

• weights

• use_best

• nli_model_name

• postprocessor

🖥️ Hardware

• device

⚡ Performance

• max_calls_per_min

• use_n_param

💻 Usage Examples

# Basic usage with default parameters
uqe = UQEnsemble(llm=llm)

# Using GPU acceleration
uqe = UQEnsemble(llm=llm, device=torch.device("cuda"))

# Custom scorer list
uqe = BlackBoxUQ(llm=llm, scorers=["bert_score", "exact_match", llm])

# High-throughput configuration with rate limiting
uqe = UQEnsemble(llm=llm, max_calls_per_min=200, use_n_param=True)

import torch

# Set the torch device
if torch.cuda.is_available():  # NVIDIA GPU
    device = torch.device("cuda")
elif torch.backends.mps.is_available():  # macOS
    device = torch.device("mps")
else:
    device = torch.device("cpu")  # CPU
print(f"Using {device.type} device")

Using cuda device

scorers = [
    "exact_match",  # Measures proportion of candidate responses that match original response (black-box)
    "noncontradiction",  # mean non-contradiction probability between candidate responses and original response (black-box)
    # "cosine_sim", # Cosine similarity between candidate responses and original response (black-box)
    "normalized_probability",  # length-normalized joint token probability (white-box)
    gpt4o_mini,  # LLM-as-a-judge (self)
    # gemini_flash, # LLM-as-a-judge (separate LLM)
]

uqe = UQEnsemble(
    llm=gpt4o_mini,
    device=device,
    max_calls_per_min=1000,
    use_n_param=True,  # Set True if using AzureChatOpenAI or ChatOpenAI for faster generation
    scorers=scorers,
)

/home/jupyter/uqlm/uqlm/scorers/white_box.py:177: UQLMDeprecationWarning: normalized_probability will be deprecated in favor of sequence_probability with length_normalize=True in v0.5
  deprecation_warning("normalized_probability will be deprecated in favor of sequence_probability with length_normalize=True in v0.5")

Method

Description & Parameters

UQEnsemble.tune

Generate responses from provided prompts, grade responses with provided grader function, and tune ensemble weights. If weights and threshold objectives match, joint optimization will happen. Otherwise, sequential optimization will happen. If an optimization problem has fewer than three choice variables, grid search will happen. Parameters: prompts - (List[str] or List[List[BaseMessage]]) A list of input prompts for the model. Note that List[List[BaseMessage]] is not compatible with judge components. ground_truth_answers - (List[str]) A list of ideal (correct) responses. grader_function - (callable, default=None) A user-defined function that takes a response and a ground truth ‘answer’ and returns a boolean indicator of whether the response is correct. If not provided, vectara’s HHEM is used: https://huggingface.co/vectara/hallucination_evaluation_model num_responses - (int, default=5) The number of sampled responses used to compute consistency. weights_objective - (str, default=’roc_auc’) Objective function for weight optimization. One of {‘fbeta_score’, ‘accuracy_score’, ‘balanced_accuracy_score’, ‘roc_auc’, ‘log_loss’, ‘average_precision’, ‘brier_score’}. Must match thresh_objective if one of {‘fbeta_score’, ‘accuracy_score’, ‘balanced_accuracy_score’}. If same as thresh_objective, joint optimization will be done. thresh_objective - (str, default=’fbeta_score’) Objective function for threshold optimization via grid search. One of {‘fbeta_score’, ‘accuracy_score’, ‘balanced_accuracy_score’}. thresh_bounds - (tuple of floats, default=(0,1)) Bounds to search for threshold. n_trials - (int, default=100) Indicates how many trials to search over with optuna optimizer step_size - (float, default=0.01) Indicates step size in grid search, if used. fscore_beta - (float, default=1) Value of beta in fbeta_score. show_progress_bars - (bool, default=True) If True, displays a progress bar while generating responses, scoring responses, and optimizing weights. Returns: UQResult containing data (prompts, responses, sampled responses, and confidence scores) and metadata 💡 Best For: Tuning an optimized ensemble for detecting hallucinations in a specific use case.

Note that below, we are providing a grader function that is specific to our use case (math questions). If you are running this example notebook with your own prompts/questions, update the grader function accordingly. Note that the default grader function, vectara/hallucination_evaluation_model, is used if no grader function is provided and generally works well across use cases.

def grade_response(response: str, answer: str) -> bool:
    return math_postprocessor(response) == answer

tune_results = await uqe.tune(
    prompts=tune_prompts,  # prompts for tuning (responses will be generated from these prompts)
    ground_truth_answers=svamp_tune["answer"],  # correct answers to 'grade' LLM responses against
    grader_function=grade_response,  # grader function to grade responses against provided answers
)

         Optimized Ensemble Weights         

==================================================

Scorer                            Weight

--------------------------------------------------

noncontradiction                  0.8341

judge_1                           0.1233

normalized_probability            0.0400

exact_match                       0.0025

==================================================

result_df = tune_results.to_df()
result_df.head(5)

	response	sampled_responses	prompt	ensemble_score	exact_match	noncontradiction	normalized_probability	judge_1
0	145	[145, 145, 145 bananas per group., 145 bananas...	When you solve this math problem only return t...	0.855957	0.6	0.976356	0.999212	0.0
1	19 pounds.	[19 pounds., 19 pounds., 19 pounds., 19 pounds...	When you solve this math problem only return t...	0.874414	1.0	1.000000	0.942262	0.0
2	$3	[$3, $3, $3, Each book cost $3., $3]	When you solve this math problem only return t...	0.991833	0.8	0.999618	0.816667	1.0
3	198	[198, 198, 198, 198, 198]	When you solve this math problem only return t...	1.000000	1.0	1.000000	1.000000	1.0
4	63 dollars.	[63 dollars., 63 dollars., 63 dollars., 63 dol...	When you solve this math problem only return t...	0.869773	0.6	0.999658	0.858838	0.0

# Save the tuned ensemble's config
uqe_tuned_config_file = "uqe_config_tuned.json"
uqe.save_config(uqe_tuned_config_file)

# # Load the tuned ensemble from the config file
# loaded_ensemble = UQEnsemble.load_config("uqe_config_tuned.json")
# loaded_ensemble.component_names, loaded_ensemble.weights, loaded_ensemble.thresh

/home/jupyter/uqlm/uqlm/utils/llm_config.py:55: LangChainBetaWarning: The method `BaseChatModel.profile` is in beta. It is actively being worked on, so the API may change.
  if attr_name.startswith("_") or callable(getattr(llm, attr_name)) or attr_name in internal_attrs or attr_name in endpoint_attrs:

3. Generate LLM Responses and Confidence Scores

To evaluate hallucination detection performance, we will generate responses and corresponding confidence scores on a holdout set using the tuned ensemble.

🔄 Class Methods: Generation + Scoring

Method	Description & Parameters
UQEnsemble.generate_and_score	Generate LLM responses, sampled LLM (candidate) responses, and compute confidence scores for the provided prompts. Parameters: prompts - (List[str] or List[List[BaseMessage]]) A list of input prompts for the model. Note that List[List[BaseMessage]] is not compatible with judge components. num_responses - (int, default=5) The number of sampled responses used to compute consistency. show_progress_bars - (bool, default=True) If True, displays a progress bar while generating and scoring responses. Returns: UQResult containing data (prompts, responses, sampled responses, and confidence scores) and metadata 💡 Best For: Complete end-to-end uncertainty quantification when starting with prompts.
UQEnsemble.score	Compute confidence scores on provided LLM responses. Should only be used if responses and sampled responses are already generated. Parameters: prompts - (List[str]) A list of input prompts for the LLM. responses - (List[str]) A list of LLM responses for the prompts. sampled_responses - (List[List[str]], default=None) A list of lists of sampled LLM responses for each prompt. These will be used to compute consistency scores by comparing to the corresponding response from responses. Must be provided if using Black-Box scorers. logprobs_results - (list of logprobs_result, default=None) List of lists of dictionaries, each returned by BaseChatModel.agenerate. Must be provided if using white box scorers. show_progress_bars - (bool, default=True) If True, displays a progress bar while scoring responses. Returns: UQResult containing data (responses, sampled responses, and confidence scores) and metadata 💡 Best For: Computing uncertainty scores when responses are already generated elsewhere.

test_results = await uqe.generate_and_score(prompts=test_prompts, num_responses=5)

4. Evaluate Hallucination Detection Performance

To evaluate hallucination detection performance, we ‘grade’ the responses against an answer key. Again, note that the grade_response function is specific to our use case (math questions). If you are using your own prompts/questions, update the grading method accordingly.

test_result_df = test_results.to_df()
test_result_df["response_correct"] = [grade_response(r, a) for r, a in zip(test_result_df["response"], svamp_test["answer"])]
test_result_df.head(5)

	response	sampled_responses	prompt	ensemble_score	exact_match	noncontradiction	normalized_probability	judge_1	response_correct
0	24	[24, 24, 24, 24, 24]	When you solve this math problem only return t...	0.876724	1.0	1.000000	0.999933	0.0	True
1	34	[34, 34, 34 campers., 34, 34 campers went rowi...	When you solve this math problem only return t...	0.997777	0.6	0.998553	0.999990	1.0	True
2	10	[10, 10, 10, 10, 10]	When you solve this math problem only return t...	1.000000	1.0	1.000000	0.999996	1.0	True
3	14 dollars.	[Each pack costs 14 dollars., Each pack costs ...	When you solve this math problem only return t...	0.995481	0.6	0.999697	0.918825	1.0	True
4	10 hours	[10 hours., 10 hours, 10 hours, 10 hours., 10 ...	When you solve this math problem only return t...	0.997702	0.4	0.999530	0.990425	1.0	True

print(f"""Baseline LLM accuracy: {np.mean(test_result_df["response_correct"])}""")

Baseline LLM accuracy: 0.89

4.1 AUROC Score

In this section, we evaluate the ability of different confidence scorers to distinguish between correct and incorrect LLM responses using the AUROC (Area Under the Receiver Operating Characteristic Curve) metric. AUROC provides a threshold-independent measure of how well each scorer ranks correct responses above incorrect ones. A higher AUROC indicates that the scorer is more effective at separating correct from incorrect outputs, making it a valuable metric for comparing the relative performance of different uncertainty estimation methods.

The plot_ranked_auc method from uqlm.utils package plots the ranked bar based on AUROC score. You can also select a subset of scorers using scorer_names(a list of strings) attribute.

plot_ranked_auc(uq_result=test_results, correct_indicators=test_result_df["response_correct"].tolist(), fontsize=12, metric_type="auroc")

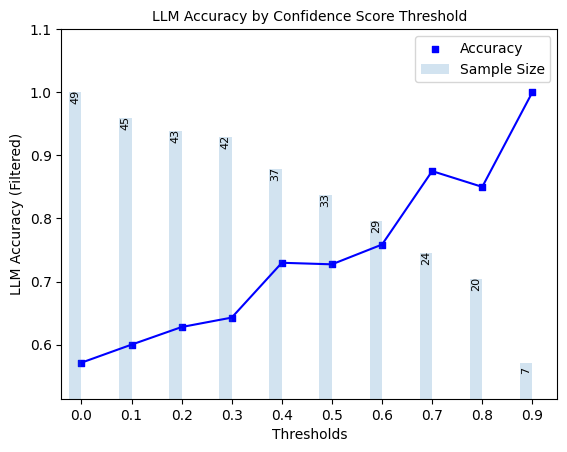
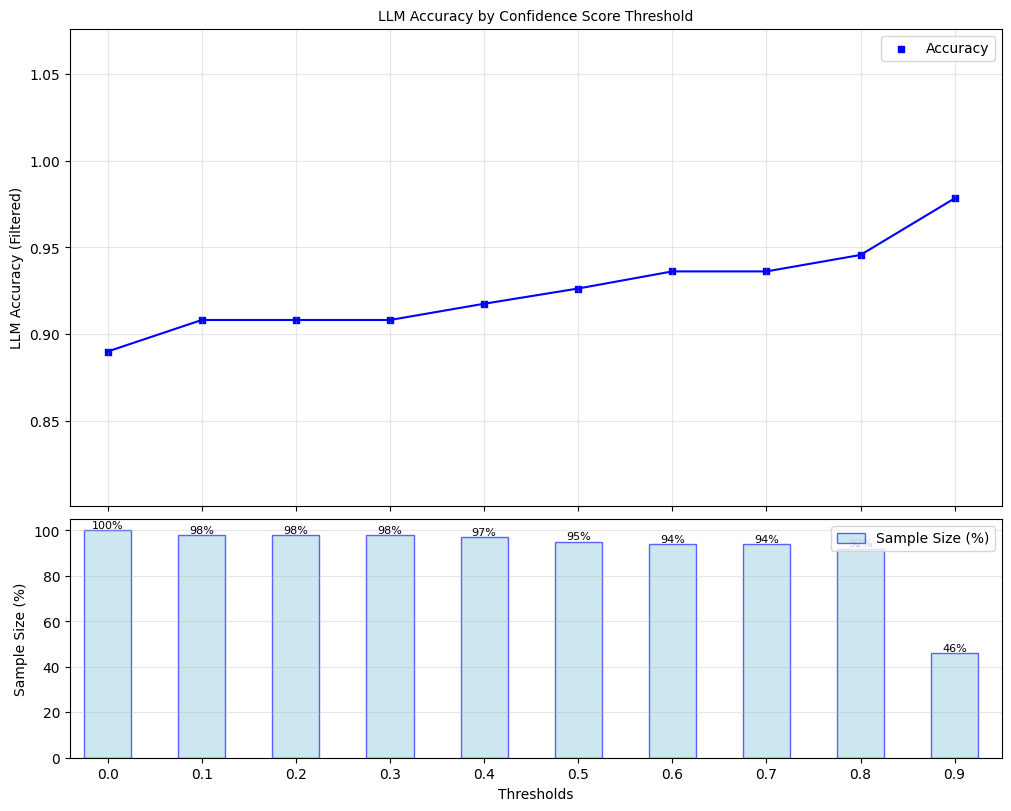
4.2 Filtered LLM Accuracy Evaluation

Here, we explore ‘filtered accuracy’ as a metric for evaluating the performance of our confidence scores. Filtered accuracy measures the change in LLM performance when responses with confidence scores below a specified threshold are excluded. By adjusting the confidence score threshold, we can observe how the accuracy of the LLM improves as less certain responses are filtered out.

We will plot the filtered accuracy across various confidence score thresholds to visualize the relationship between confidence and LLM accuracy. This analysis helps in understanding the trade-off between response coverage (measured by sample size below) and LLM accuracy, providing insights into the reliability of the LLM’s outputs.

Here, we plot the results for the ensemble scorer.

plot_model_accuracies(scores=test_result_df.ensemble_score, correct_indicators=test_result_df.response_correct, display_percentage=True)

4.3 Precision, Recall, F1-Score of Hallucination Detection

Lastly, we compute the optimal threshold for binarizing confidence scores, using F1-score as the objective. Using this threshold, we compute precision, recall, and F1-score for ensemble predictions of whether responses are correct.

# extract optimal threshold
best_threshold = uqe.thresh

# Define score vector and corresponding correct indicators (i.e. ground truth)
y_scores = test_result_df["ensemble_score"]  # confidence score
correct_indicators = (test_result_df.response_correct) * 1  # Whether responses is actually correct
y_pred = [(s > best_threshold) * 1 for s in y_scores]  # predicts whether response is correct based on confidence score
print(f"Ensemble F1-optimal threshold: {best_threshold}")

Ensemble F1-optimal threshold: 0.74

# print results
header = f"{'Metrics':<25}" + f"{'Ensemble':<25}"
print("=" * len(header) + "\n" + header + "\n" + "-" * len(header))
print(f"{'Precision':<25}{round(precision_score(y_true=correct_indicators, y_pred=y_pred), 3):<25})")
print(f"{'Recall':<25}{round(recall_score(y_true=correct_indicators, y_pred=y_pred), 3):<25}")
print(f"{'F1-score':<25}{round(f1_score(y_true=correct_indicators, y_pred=y_pred), 3):<25}")
print("-" * len(header))
print(f"{'F-1 optimal threshold':<25}{best_threshold:<25}")
print("=" * len(header))

==================================================
Metrics                  Ensemble
--------------------------------------------------
Precision                0.935                    )
Recall                   0.978
F1-score                 0.956
--------------------------------------------------
F-1 optimal threshold    0.74
==================================================

5. Scorer Definitions

Black-Box Scorers

Black-Box UQ scorers exploit variation in LLM responses to the same prompt to measure semantic consistency. All scorers have outputs ranging from 0 to 1, with higher values indicating higher confidence.

For a given prompt \(x_i\), these approaches involves generating \(m\) responses \(\tilde{\mathbf{y}}_i = \{ \tilde{y}_{i1},...,\tilde{y}_{im}\}\), using a non-zero temperature, from the same prompt and comparing these responses to the original response \(y_{i}\). We provide detailed descriptions of each below.

Non-Contradiction Probability (noncontradiction)

Non-contradiction probability (NCP) computes the mean non-contradiction probability estimated by a natural language inference (NLI) model. This score is formally defined as follows:

\[NCP(y_i; \tilde{\mathbf{y}}_i) = 1 - \frac{1}{m} \sum_{j=1}^m\frac{p_{contra}(y_i, \tilde{y}_{ij}) + p_{contra}(y_i, \tilde{y}_{ij})}{2}.\]

Above, \(p_{contra}(y_i, \tilde{y}_{ij})\) denotes the (asymmetric) contradiction probability estimated by the NLI model for response \(y_i\) and candidate \(\tilde{y}_{ij}\). For more on this scorer, refer to Chen & Mueller, 2023, Lin et al., 2024, or Manakul et al., 2023.

Entailment Probability (entailment)

Entailment probability (EP) computes the mean entailment probability estimated by a natural language inference (NLI) model. This score is formally defined as follows:

\[EP(y_i; \tilde{\mathbf{y}}_i) = \frac{1}{m} \sum_{j=1}^m\frac{p_{entail}(y_i, \tilde{y}_{ij}) + p_{entail}(y_i, \tilde{y}_{ij})}{2}.\]

Above, \(p_{entail}(y_i, \tilde{y}_{ij})\) denotes the (asymmetric) entailment probability estimated by the NLI model for response \(y_i\) and candidate \(\tilde{y}_{ij}\). We adapt this scorer from Chen & Mueller, 2023, Lin et al., 2024.

Normalized Semantic Negentropy (semantic_negentropy)

Normalized Semantic Negentropy (NSN) normalizes the standard computation of discrete semantic entropy to be increasing with higher confidence and have [0,1] support. In contrast to the EMR and NCP, semantic entropy does not distinguish between an original response and candidate responses. Instead, this approach computes a single metric value on a list of responses generated from the same prompt. Under this approach, responses are clustered using an NLI model based on mutual entailment. We consider the discrete version of SE, where the final set of clusters is defined as follows:

\[SE(y_i; \tilde{\mathbf{y}}_i) = - \sum_{C \in \mathcal{C}} P(C|y_i, \tilde{\mathbf{y}}_i)\log P(C|y_i, \tilde{\mathbf{y}}_i),\]

where \(P(C|y_i, \tilde{\mathbf{y}}_i)\) denotes the probability a randomly selected response $y \in `{y_i} :nbsphinx-math:cup :nbsphinx-math:tilde{mathbf{y}}`_i $ belongs to cluster \(C\), and \(\mathcal{C}\) denotes the full set of clusters of \(\{y_i\} \cup \tilde{\mathbf{y}}_i\).

To ensure that we have a normalized confidence score with \([0,1]\) support and with higher values corresponding to higher confidence, we implement the following normalization to arrive at Normalized Semantic Negentropy (NSN):

\[NSN(y_i; \tilde{\mathbf{y}}_i) = 1 - \frac{SE(y_i; \tilde{\mathbf{y}}_i)}{\log m},\]

where \(\log m\) is included to normalize the support. For more on discrete semantic entropy, refer to Farquhar et al., 2024; Kuhn et al., 2023, and for more on our normalized version, refer to Bouchard & Chauhan, 2025.

Number of Semantic Sets (num_semantic_sets)

Number of Semantic Sets counts the number of unique response sets (clusters) obtained during the computation of semantic entropy, as defined above. Let \(N_C\) denote the number of unique semantic clusters and \(m\) denote the number of sampled responses. We normalize this count to obtain a confidence score, Semantic Sets Confidence (SSC) in \([0,1]\) as follows:

\[SSC(y_i; \tilde{\mathbf{y}}_i) = 1 - \frac{N_C - 1}{m - 1}.\]

Note that when \(N_C=1\), all sampled responses are semantically equivalent, so the confidence score is 1, and when \(N_C=m\), all responses are semantically distinct, so the confidence score is 0. For more on Number of Semantic Sets, refer to Lin et al., 2024; Vashurin et al., 2025; Kuhn et al., 2023.

BERTScore (bert_score)

Let a tokenized text sequence be denoted as \(\textbf{t} = \{t_1,...t_L\}\) and the corresponding contextualized word embeddings as \(\textbf{E} = \{\textbf{e}_1,...,\textbf{e}_L\}\), where \(L\) is the number of tokens in the text. The BERTScore precision, recall, and F1-scores between two tokenized texts \(\textbf{t}, \textbf{t}'\) are respectively defined as follows:

\[BertP(\textbf{t}, \textbf{t}') = \frac{1}{| \textbf{t}|} \sum_{t \in \textbf{t}} \max_{t' \in \textbf{t}'} \textbf{e} \cdot \textbf{e}'\]

\[BertR(\textbf{t}, \textbf{t}') = \frac{1}{| \textbf{t}'|} \sum_{t' \in \textbf{t}'} \max_{t \in \textbf{t}} \textbf{e} \cdot \textbf{e}'\]

\[BertF(\textbf{t}, \textbf{t}') = 2\frac{ BertP(\textbf{t}, \textbf{t}') BertR(\textbf{t}, \textbf{t}')}{BertPr(\textbf{t}, \textbf{t}') + BertRec(\textbf{t}, \textbf{t}')},\]

where \(e, e'\) respectively correspond to \(t, t'\). We compute our BERTScore-based confidence scores as follows:

\[BertConfidence(y_i; \tilde{\mathbf{y}}_i) = \frac{1}{m} \sum_{j=1}^m BertF(y_i, \tilde{y}_{ij}),\]

i.e. the average BERTScore F1 across pairings of the original response with all candidate responses. For more on BERTScore, refer to Zheng et al., 2020.

Normalized Cosine Similarity (cosine_sim)

This scorer leverages a sentence transformer to map LLM outputs to an embedding space and measure similarity using those sentence embeddings. Let \(V: \mathcal{Y} \xrightarrow{} \mathbb{R}^d\) denote the sentence transformer, where \(d\) is the dimension of the embedding space. The average cosine similarity across pairings of the original response with all candidate responses is given as follows:

\[CS(y_i; \tilde{\mathbf{y}}_i) = \frac{1}{m} \sum_{i=1}^m \frac{\mathbf{V}(y_i) \cdot \mathbf{V}(\tilde{y}_{ij}) }{ \lVert \mathbf{V}(y_i) \rVert \lVert \mathbf{V}(\tilde{y}_{ij}) \rVert}.\]

To ensure a standardized support of \([0, 1]\), we normalize cosine similarity to obtain confidence scores as follows:

\[NCS(y_i; \tilde{\mathbf{y}}_i) = \frac{CS(y_i; \tilde{\mathbf{y}}_i) + 1}{2}.\]

White-box UQ scorers leverage token probabilities of the LLM’s generated response to quantify uncertainty. All scorers have outputs ranging from 0 to 1, with higher values indicating higher confidence. We define two white-box UQ scorers below.

Length-Normalized Token Probability (normalized_probability)

Let the tokenization LLM response \(y_i\) be denoted as \(\{t_1,...,t_{L_i}\}\), where \(L_i\) denotes the number of tokens the response. Length-normalized token probability (LNTP) computes a length-normalized analog of joint token probability:

\[LNTP(y_i) = \prod_{t \in y_i} p_t^{\frac{1}{L_i}},\]

where \(p_t\) denotes the token probability for token \(t\). Note that this score is equivalent to the geometric mean of token probabilities for response \(y_i\). For more on this scorer, refer to Malinin & Gales, 2021.

Minimum Token Probability (min_probability)

Minimum token probability (MTP) uses the minimum among token probabilities for a given responses as a confidence score:

\[MTP(y_i) = \min_{t \in y_i} p_t,\]

where \(t\) and \(p_t\) follow the same definitions as above. For more on this scorer, refer to Manakul et al., 2023.

Under the LLM-as-a-Judge approach, either the same LLM that was used for generating the original responses or a different LLM is asked to form a judgment about a pre-generated response. Below, we define two LLM-as-a-Judge scorer templates. ### Ternary Judge Template (true_false_uncertain) We follow the approach proposed by Chen & Mueller, 2023 in which an LLM is instructed to score a question-response concatenation as either incorrect, uncertain, or correct using a carefully constructed prompt. These categories are respectively mapped to numerical scores of 0, 0.5, and 1. We denote the LLM-as-a-judge scorers as \(J: \mathcal{Y} \xrightarrow[]{} \{0, 0.5, 1\}\). Formally, we can write this scorer function as follows:

J(y_i) =

We modify the ternary approach above and include only two categories: Correct or Incorrect, which respectively map to 1 and 0.

For the continuous template, the LLM is asked to directly score a question-response concatenation’s correctness on a scale of 0 to 1.

Here the judge is asked to score a question-response concatenation on a 5-point likert scale. We convert these likert scores to a [0,1] scale as follows:

J(y_i) =

© 2025 CVS Health and/or one of its affiliates. All rights reserved.